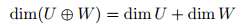기계 학습을 위한 수학: 선형 대수학 시리즈. 기계 학습을 위한 수학그리고 길버트 스트랭스 교수 선형 대수학참조.
벡터 공간
벡터 공간은 벡터들로 이루어진 공간으로 선형대수학을 공부할 때 주로 다루는 기본 공간이다. 벡터 공간에는 덧셈과 곱셈의 두 연산자가 정의됩니다. 이를 통해 벡터를 더하거나 스칼라 값을 곱할 수 있습니다. 벡터 공간에는 다음과 같은 속성이 있습니다.
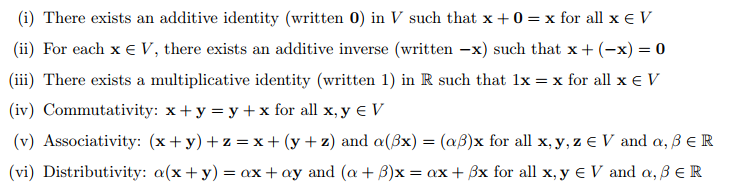
기계 학습에서 다루는 주요 영역은 다음과 같습니다. 유클리드 공간, 실수로 구성된 벡터로 구성된 공간입니다. 종종 $R^n$이라고 부르며 $n * 1$ 크기의 행렬로 생각하는 것이 안전합니다. 벡터 공간이기 때문에 위에서 정의한 속성을 모두 만족합니다.
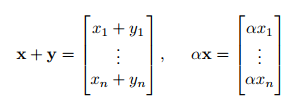
부분 공간
벡터 공간은 다른 벡터 공간을 포함할 수 있으며, 이 경우 포함된 공간을 V의 부분 공간이라고 합니다. 부분 공간에는 다음과 같은 속성이 있습니다(덧셈과 곱셈을 위한 닫힌 공간). 모든 벡터 공간에는 하위 공간이 있으며 공통 하위 공간은 {0}입니다.

벡터공간 V의 부분공간인 U와 W를 더하면 다음과 같이 표현할 수 있다.
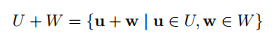
U와 W는 V의 부분공간이므로 U+W도 V의 부분공간입니다. 위의 예와 함께 직접 합계(⊕)연산자를 살펴보겠습니다. 직접 합계(⊕). 두 부분 공간의 일반적인 합은 다음과 같이 표현됩니다.
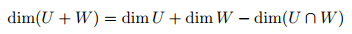
두 부분 공간의 교차가 없을 때 이를 직접 합이라고 하는 것으로 표현할 수 있습니다.